Стохастические сверхнизкочастотные колебания интенсивности люминесценции с поверхности полимерной мембраны, набухающей в водных растворах солей

Н.Ф. Бункин¹ ², П.Н. Болоцкова¹ ², Е.В. Бондарчук³, В.Г. Грязнов³, В.А. Козлов¹ ², М.А. Окунева¹ ², О.В. Овчинников³, О.П. Смолий³, И.Ф. Турканов³, Е.А.Галкина³, А.С. Дмитриев⁴, А.Ф. Селиверстов⁵

¹Московский государственный технический университет им. Н. Э. Баумана, 2-я Бауманская ул. 5, Москва 105005, Россия;
²Институт общей физики им. А.М. Прохорова РАН, ул. 38, Москва 119991, Россия
³«Концерн ГРАНИТ», Гоголевский бул., 31, корп. 2, Москва 119019, Россия;
⁴Институт радиотехники и электроники РАН им. Котельникова, ул. Моховая, д. 11, стр. 7, 125009 14 Москва, Россия
⁵Институт физической химии и электрохимии им. Фрумкина РАН, Ленинский проспект, д. 31, стр. 4, 16 Москва, 119071, Россия

Статья опубликована в журнале Polymers (рейтинг — Q1) 11 февраля 2022 года.
Ссылка на статью на английском

АННОТАЦИЯ

Исследована фотолюминесценция с поверхности полимерной мембраны Нафион при набухании в изотонических водных растворах и воде Milli-Q.

Жидкие образцы предварительно обрабатывали электрическими импульсами длительностью 1 мкс и с амплитудой 0,1 В с помощью антенны в виде плоского конденсатора; эксперименты по фотолюминесцентной спектроскопии проводились через 20 мин после такой обработки. Типичная зависимость интенсивности люминесценции I от времени набухания t подчиняется экспоненциально затухающей функции.

Характерное время затухания этих функций и стационарный уровень интенсивности люминесценции зависят от частоты следования электрических импульсов, и полученные зависимости хорошо воспроизводятся.

Оказалось, что при определенных частотах следования импульсов зависимость I(t) является случайной функцией и воспроизводимость отсутствует. Стохастические эффекты связаны со случайной внешней силой электромагнитной природы, действующей на полимерную мембрану в процессе набухания. Источником этой случайной силы, по нашему мнению, являются низкочастотные пульсации нейтронных звезд или белых карликов.

1. ВВЕДЕНИЕ

Нафион™ (C₇HF₁₃O₅S х C2F4) состоит из групп перфторвинилового эфира, оканчивающихся сульфоновыми группами, на основной цепи из тетрафторэтилена (тефлона). Тефлон очень гидрофобен, в то время как сульфоновые группы, по существу, гидрофильны.

При набухании в водной среде возникает наноструктура, состоящая из цилиндрических обратных мицелл. Внутри нафионовой мембраны образуются заполненные водой каналы диаметром 2-3 нм; см. работу [1] для получения подробной информации.

Полимерная мембрана Нафион широко изучается в различных областях, таких как физика, химия и водородная энергетика (см., например, список литературы [2 – 6], относящийся к статьям, опубликованным в 2021 г.). Большинство методик, применяемых для исследования нафиона, ориентированы на изучение объемных свойств полимера. В то же время исследовалась и вода, прилегающая к набухшей поверхности полимера, см. недавние работы [7 – 10] и монографию [11], описывающие опыты, в которых нафионовая мембрана погружается в водную суспензию коллоидных микросфер.

Оказалось, что микросферы отталкиваются от мембраны на расстояние в несколько сотен микрон. Область, из которой эффективно вытесняются коллоидные микросферы, получила название «зона отчуждения» (ЗО). Феномен ЗО может иметь важное инженерное применение в фильтрации воды, уменьшении биологического обрастания и микрогидродинамике [13]. Феномен ЗО также имеет очевидное значение для понимания биологических систем и решения нерешенных вопросов о «биологической воде» [14]. В соответствии с моделью, развитой в монографии [11], поверхность Нафиона придает квазикристаллическую структуру в макроскопическом масштабе соседним слоям воды; в монографии [11] (см. также многочисленные ссылки там) этот эффект назван образованием «четвертой фазы» воды.

Ширина зоны отчуждения составляет около 300 мкм. Это удивительно и не поддается объяснению с помощью стандартных физико-химических теорий. Некоторые физические механизмы, которые могут быть ответственны за формирование ЗО, обсуждаются в недавнем обзоре [15]. Как было показано в нашей недавней работе [16], при набухании нафиона в воде полимерные волокна разматываются в объем воды, но не отрываются полностью от поверхности мембраны, образуя жесткую щеткообразную структуру. Таким образом, согласно нашей модели, ЗО не является особой фазой воды, а коллоидные микросферы выталкиваются из области, прилегающей к мембране, за счет разматывания полимерных волокон.

Очень важно, что эффект раскручивания зависит от содержания дейтерия в жидком образце, подробнее см. [16]. В действительности для обычной природной воды (содержание дейтерия 157 ± 1 ч./млн, см. [17]) размер ЗО составляет до нескольких сотен микрон за счет разматывания, а для так называемой обедненной дейтерием воды (DDW, содержание дейтерия ≤ 1 ч./млн), эффект раскручивания отсутствует и размер ЗО равен нулю. Учитывая, что мембрана Нафион «украшена» размотанными полимерными волокнами, мы видим явную аналогию с мембраной клетки человека. Действительно, структура каналов в массе полимера подобна липидному бислою, а размотанные волокна подобны гликокаликсу (внеклеточному матриксу) и эндотелиальному поверхностному слою сосудистой ткани человека, см., например, [18]. Это вопрос чрезвычайной важности для физиологии, см. [19]. Развивая аналогию между клеточной мембраной человека и мембраной Нафион, отметим, что существует ряд органических соединений, стимулирующих проникновение различных ионов через катионные каналы клеточной мембраны.

Можно сказать, что полимерная мембрана Нафион аналогична синтетическим биологическим полимерным мембранам, см. недавний обзор [20]. В связи с этим особый интерес для изучения представляет алкалоид пиперин (C₁₇H₁₉NO₃), стимулирующий проводимость ионов кальция [21] и калия [22] в клеточных каналах человека. Действительно, поскольку мембрана Нафиона содержит отрицательно заряженные каналы, являющиеся проводниками протонов, очень важно изучить взаимодействие пиперина с Нафионом.Одной из целей данной работы является выяснение механизмов взаимодействия клеточных мембран с неионизирующим низкочастотным электромагнитным излучением. Это взаимодействие лежит в основе лечения различных заболеваний низкочастотным электромагнитным полем, см. [23 – 30]. Процитированные монографии и обзоры подтверждают эффективность данной методики. Эти работы написаны в основном врачами, применяющими данную методику в своей медицинской практике; физическая природа низкочастотного воздействия на живую ткань обычно не обсуждается. В рамках аналогии между клеточной мембраной и мембраной Нафиона представляет интерес изучение особенностей взаимодействия Нафиона с низкочастотным электромагнитным излучением.

Наша группа выполнила ряд экспериментов по влиянию низкочастотного электромагнитного облучения изотонических растворов, в которых затем замачивали мембрану Нафион, см. [31]. Как показано в [31], характерное время набухания полимерной мембраны различно для облученных и необлученных (контрольных) жидких образцов. Интервал времени между электромагнитной обработкой и измерением эффектов облучения составлял около 20 мин. Целью данного исследования является выяснение механизмов взаимодействия полимерной мембраны с изотоническими растворами с низкочастотным электромагнитным излучением, что может быть использовано в медицинской практике. В данной работе мы выполнили ряд экспериментов по фотолюминесцентной спектроскопии, где подробно исследовали диапазон частот следования электрических импульсов от 5 Гц до 500 кГц с интервалом 5 Гц; если на определенных частотах обнаруживались какие-либо особенности в динамике набухания полимера (см. ниже), соответствующий частотный интервал пройден с шагом 1 Гц.

В некоторых экспериментах мы накрывали нашу экспериментальную установку алюминиевой фольгой. Кроме того, исследовались жидкие образцы с различным изотопным составом. Это позволило обнаружить ряд изолированных частот электромагнитного воздействия, при котором интенсивность люминесценции, обычно описываемая регулярной функцией времени, проявляет спорадический характер во времени.

Новизна нашей работы заключается в исследовании спектральных характеристик стохастической динамики люминесценции и качественной теоретической модели, лежащей в основе стохастических режимов, объясняющих различия кинетики набухания полимера в обычной воде и DDW. Полученные результаты могут быть использованы для уточнения механизмов взаимодействия полимерной мембраны с изотоническими растворами различного изотопного состава в поле внешнего низкочастотного облучения, что может найти применение в медицинской практике.

2. МАТЕРИАЛЫ И МЕТОДЫ

2.1. Материалы

Мы исследовали пластины мембраны Нафион N117 (Sigma Aldrich, Сент-Луис, Миссури, США) толщиной 175 мкм и площадью 1х1 см². Пластины Нафион замачивали в воде Milli-Q с удельным сопротивлением 4 МОм х см (измерения проводились через 1 ч после приготовления кондуктометром CON270043S Eutech, Thermo Fisher Scientific, Waltham, MA, USA), а также в изотоническом растворе NaCl (0,9 %; Мосфарм, Московская область, Россия) и растворе Рингера (Биосинтез, Пенза, Россия). В нашем случае раствор Рингера состоял из NaCl (8,6 г/л), KCl (0,3 г/л) и CaCl₂ х 6H₂O (0,25 г/л), растворенных в воде. Содержание дейтерия в этих образцах составило 157 ± 1 ч./млн. В некоторых случаях для приготовления 0,9 % растворов NaCl на основе воды, обедненной дейтерием (DDW; содержание дейтерия ≤ 1 ч./млн, Sigma Aldrich, Сент-Луис, Миссури, США) использовался ЧДА NaCl (Sigma Aldrich, Сент-Луис, Миссури, США). Пиперин (C₁₇H₁₉NO₃), 98 %, был приобретен у CheMondis GmbH, Кельн, Германия. Смеси пиперина готовили в растворе Рингера с концентрацией 40 мг/л; эта концентрация соответствует насыщенной смеси.

2.2. Инструменты

2.2.1. Подготовка жидких образцов

Для изучения эффектов электромагнитного воздействия была разработана экспериментальная установка, позволяющая воздействовать на жидкие образцы электрическими импульсами положительной/отрицательной полярности с частотой следования от 5 Гц до 500 кГц с возможностью изменения амплитуды импульсов; длительность импульса составляла 1 мкс. Фотография этой установки представлена на рис. 1 (а) и (б).

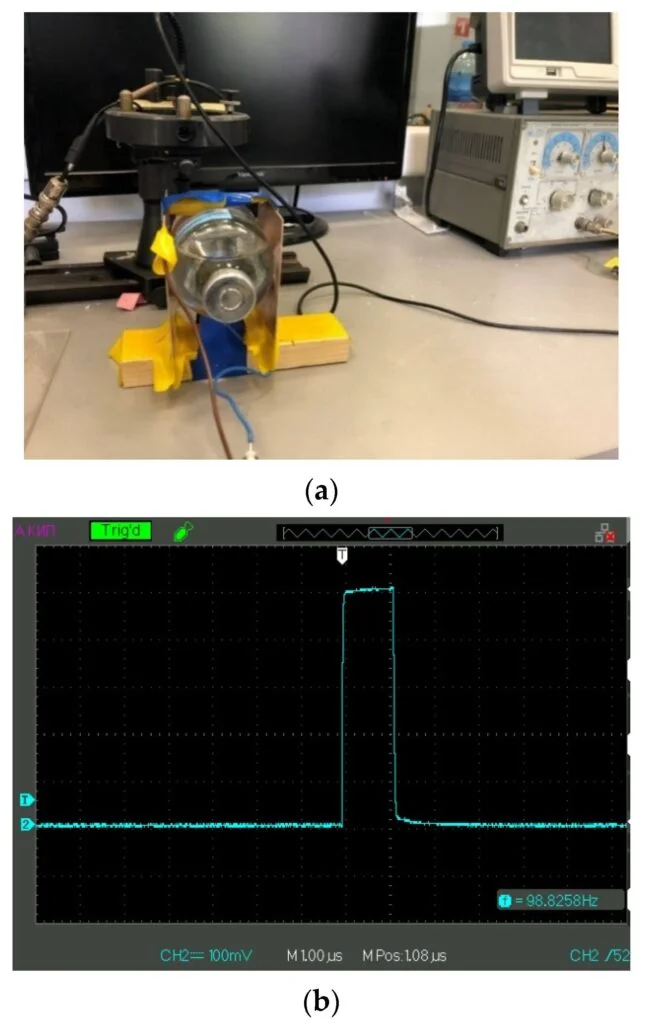
Рисунок 1. Панель (б) — форма электрического импульса, подаваемого на пластины конденсатора.

В этих экспериментах использовали генератор импульсов Г5-63 (Россия) и осциллограф АКИП 4115/3А (Россия). Эта установка позволяла облучать жидкие образцы в бесконтактном режиме, см. рис. 1 (а). В стеклянную кювету объемом 200 мл помещали исследуемые жидкие образцы. Эта кювета помещалась внутрь планарного конденсатора, площадь электродов которого составляла 100 см2, расстояние между ними 5 см, т. е. емкость была 1,77 пФ.

Представленные ниже результаты относятся к амплитуде импульса 100 мВ, см. рис. 1 (б). Жидкие образцы подвергались воздействию электрических импульсов в течение 20 минут (время обработки). После облучения жидкого образца обработанная жидкость заливалась в кювету, показанную на рис. 2, для исследования сигнала фотолюминесценции с пластины Нафион. Интервал между окончанием обработки электрическими импульсами и началом эксперимента с люминесценцией составлял ~ 20 минут.

Принято считать, что характерные времена релаксации в воде и водных растворах ограничены временем жизни водородной связи, составляющим около пикосекунды, см., например, [32].

Таким образом, казалось бы вероятным, что все эффекты, связанные с электромагнитным воздействием, не должны проявляться через 20 минут после этого воздействия.

2.2.2. Исследование фотолюминесценции

В этом подразделе мы кратко опишем протокол экспериментов по фотолюминесценции; подробнее см. [16, 31]. Методика основана на возбуждении люминесценции с поверхности Нафиона за счет накачки в УФ-диапазоне. Для возбуждения люминесценции необходимо облучить вещество в пределах одной из его полос поглощения. Известно [33], что максимумы поглощения Нафиона сосредоточены на длине волны λ = 270 нм. Известно также (см., например, [34]), что вода в этом спектральном диапазоне не поглощает. В наших экспериментах по фотолюминесценции мы использовали излучение с длиной волны λ = 369 нм, соответствующей длинноволновой области указанной полосы поглощения. В параллельных экспериментах (см. [16]) было установлено, что концевые сульфогруппы HSO₃ служат центрами люминесценции нафиона при УФ-облучении.

Как показали опыты с раствором Нафиона в изопропаноле (см. [16]), интенсивность люминесценции I линейно растет с увеличением объемной плотности частиц нафиона nNaf и может быть выражена как:

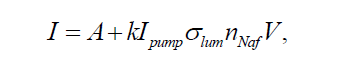
где nNaf – объемная плотность центров люминесценции, т.е. терминальных сульфогрупп HSO₃. Поскольку эти группы присоединены к полимерным цепям, nNaf можно связать с объемной плотностью частиц Нафиона. Здесь Ipump — интенсивность накачки, A = 20 — 270 усл. ед. соответствует спектральной плотности шума миниспектрометра и рассеянной засветки в относительных единицах, k — коэффициент передачи установки, V — объем люминесценции, σlum – сечение люминесценции (спектральный максимум σlum соответствует λ = 460 нм). Линейная зависимость интенсивности люминесценции I от nNaf реализуется при условии, что σlum = const.
Для проведения экспериментов по спектроскопии фотолюминесценции была сконструирована установка (подробнее см. [13]). Схема установки представлена на рис. 2.

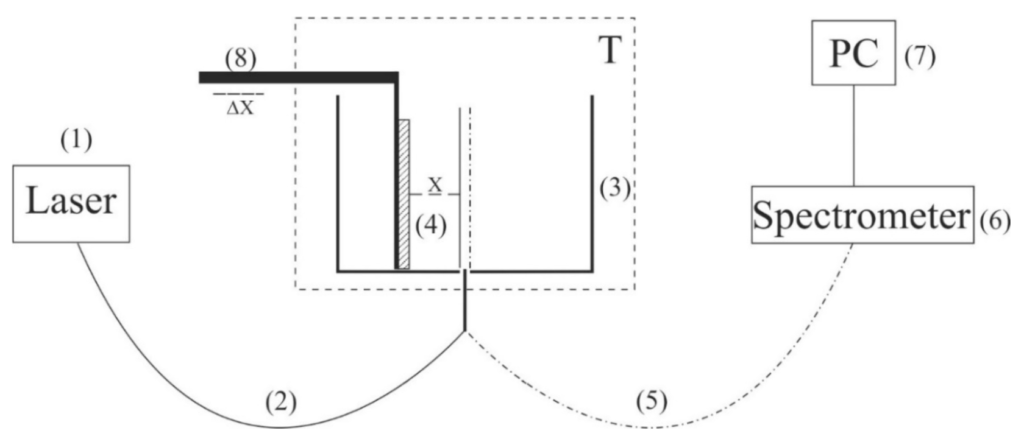
Рисунок 2. Схема экспериментальной установки для лазерной люминесцентной спектроскопии. Комментарии в тексте.

Зондирующее излучение лазерного диода непрерывного действия (1) (оптическая накачка) на длине волны λ = 369 нм вводилось в многомодовый кварцевый световод (2) диаметром ø = 100 мкм с числовой апертурой NA = n • sin α = 0,3, где n = 1 — показатель преломления в воздухе, α — угол расходимости пучка на выходе свето-вода в воздухе. Волокно закреплялось в отверстии в центре дна цилиндрической кюветы (3) из тефлона; направление луча накачки задавало оптическую ось экспериментальной установки. Кювета была термостабилизирована при комнатной температуре (T = 23°C) с точностью ± 0,1°C и заполнена образцом исследуемой жидкости. Исследовали набухание квадратной пластины Нафиона (4) со стороной h = 10 мм и толщиной d = 175 мкм. Пластина крепилась параллельно оптической оси, т. е. эксперименты проводились в геометрии скользящего падения. Края пластины нафион плотно фиксировали двумя зажимами; никаких дополнительных средств для фиксации пластины не применялось.

Размер зажимов был много меньше ширины пластины нафиона, т. е. реализовывалось приближение условий свободной границы. Кроме того, в процессе набухания толщина пластины нафиона могла увеличиваться; этот эффект был минимизирован за счет жесткой фиксации пластины.

В начале опыта в пустую кювету помещали сухую (безводную) пластину Нафиона; мы могли перемещать пластину горизонтально с помощью шагового двигателя (8), тем самым изменяя положение пластины относительно оптической оси. При этом мы добивались максимума сигнала люминесценции; такое положение пластины Нафиона считалось оптимальным. При заливке жидкого образца в кювету первоначально гидрофобная пластина Нафиона изгибалась вдоль оптической оси.

Однако такой изгиб приводил лишь к эффективному смещению границы Нафион — вода (это смещение составило около 1 мм), но не приводил к изменению угла падения излучения накачки. Для восстановления оптимального положения пластины относительно оптической оси проводилась дополнительная регулировка с помощью шагового двигателя (8). Излучение люминесценции отражалось внутренней поверхностью кюветы (Нафион прозрачен в видимом диапазоне) и концентрировалось вдоль оптической оси кюветы. Это привело к значительному увеличению интенсивности люминесценции.

Сигнал люминесценции принимался кварцевым волокном (5), закрепленным в центре кюветы, и передавался на миниспектрометр (6) ФСД-8 (Россия). Экспериментальные данные накапливались на компьютере (7). В эксперименте исследовали временную динамику интенсивности люминесценции в ее спектральном максимуме (λ = 460 нм) в зависимости от времени замачивания нафиона в исследуемой жидкости. Начало отсчета времени замачивания t соответствует моменту заливки жидкой пробы в кювету.

3. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

На рис. 3 (а) – (в) приведены типичные зависимости I в ее спектральном максимуме (λ = 460 нм) от времени набухания t в воде Milli-Q, изотонических растворах NaCl и Рингера; для определенности здесь приведены зависимости для частоты следования импульсов 60 Гц. Также показаны эталонные кривые для необработанных (контрольные) образцов.

Экспериментальные точки соответствуют усреднению по пяти последовательным измерениям. На всех графиках указаны доверительные интервалы. Все полученные зависимости хорошо аппроксимируются одной экспоненциальной функцией с характерными временами затухания τ, соответствующие формулы приведены на вставках и выделены разными цветами. Как следует из графиков, эталонные зависимости описываются примерно одинаковыми показателями степени: Y = 14366 + 47655 • exp (−t /14) для воды, Y = 13239 + 45548 • exp (−t /14) для раствора NaCl, Y = 18937 + 48400 • exp (−t / 13) для раствора Рингера, т.е. ионные добавки практически не повлияли бы на динамику набухания Нафиона.

В данном случае интенсивность люминесценции во всех обработанных образцах ниже, чем в контрольных образцах. Отметим, что при некоторых частотах следования импульсов ситуация меняется, т. е. интенсивность люминесценции в обработанных образцах может превышать эталонную зависимость или с хорошей точностью совпадать с эталонной кривой. Основная особенность полученных результатов: интенсивность люминесценции I(t) после обработки описывается одной экспоненциальной функцией, а полученные результаты имеют достаточно хорошую воспроизводимость. Аналогичные результаты (на других частотах) были представлены в [31], поэтому мы не будем здесь подробно останавливаться на этом.

Экспоненциальная зависимость I(t) означает, что сечение люминесценции σlum постоянно. Действительно, если предположить, что объемная плотность nNaf центров люминесценции (в нашем случае сульфогрупп) подчиняется уравнению (1), т. е. nNaf в приповерхностном слое полимерной мембраны уменьшается за счет проникновения в этот слой молекул воды, можно записать:

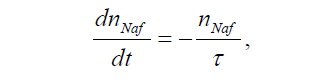
где τ – характерное время набухания. Таким образом, мы получаем:

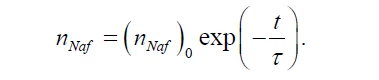
Поскольку I(t) пропорциональна nNaf (см. уравнение (1)), она должна экспоненциально затухать.

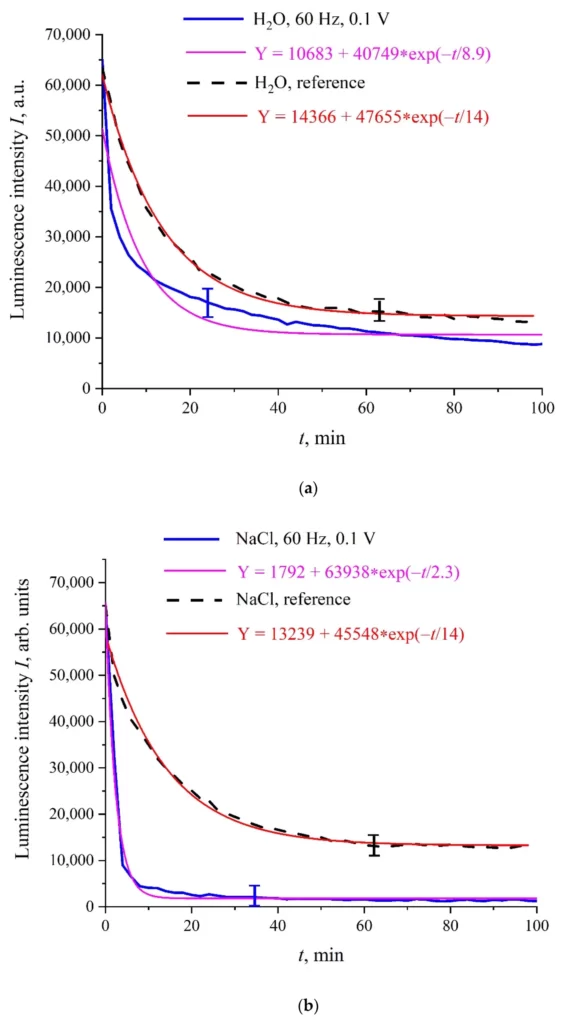
Рисунок 3. Зависимость интенсивности люминесценции I в спектральном максимуме от времени пропитки полимерной мембраны t для жидких образцов, обработанных электрическими импульсами амплитудой 100 мВ с частотой следования 60 Гц; необработанные (контрольные) образцы выделены пунктирной линией; (а) — вода Milli-Q; (b) — раствор NaCl; (c) — раствор Рингера.

Мы видим, что обработка жидких образцов электрическими импульсами не приводит к существенным изменениям кинетики набухания полимера: после обработки сохраняется экспоненциальный характер I(t). Однако оказалось, что добавление некоторых органических соединений к исследуемым жидким образцам может привести к нарушению экспоненциального поведения I(t), не требующему обработки электрическими импульсами. На рис. 4 представлена зависимость I(t) для смеси «раствор Рингера — пиперин» с концентрацией пиперина 40 мг/л (насыщенная смесь).

Мы видим, что в этом случае зависимость I(t) достаточно случайна; результаты более детальных исследований смесей пиперина в воде и изотонических растворах, в том числе при обработке жидких образцов электрическими импульсами, будут опубликованы в другом месте. Для нас важно, что стохастический характер в поведении I(t) может возникать, например, при добавлении в исследуемые жидкости некоторых органических соединений.

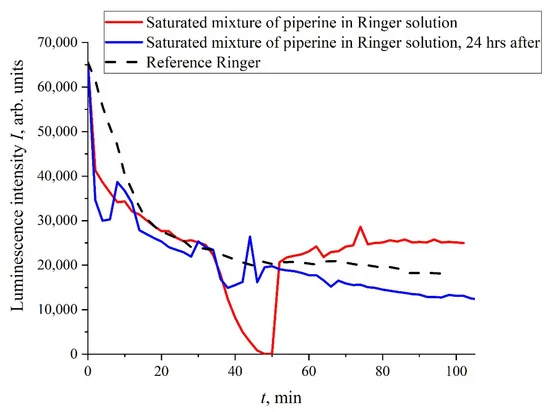
Рисунок 4. Зависимость I(t) для изотонического раствора Рингера, содержащего пиперин с концентрацией 40 мг/л (насыщенная смесь). Красная кривая относится к измерениям сразу после разбавления пиперина, а синяя кривая относится к тем же измерениям, выполненным через 24 часа.

В дальнейшем мы будем рассматривать только изотонический раствор NaCl. На рис. 5 представлены зависимости интенсивности люминесценции I(t) в спектральном максимуме для частот следования импульсов 400 и 440 Гц. В отличие от ситуации, изображенной на рис. 4, графики на рис. 5 достаточно близки к эталонным кривым и описываются затухающими экспоненциальными функциями, которые хорошо воспроизводятся.

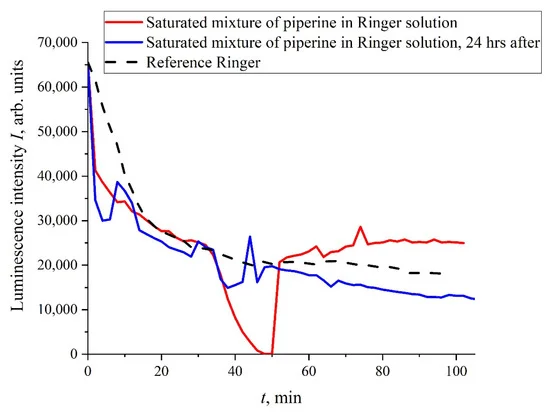
Рисунок 5. Зависимость I(t) для растворов NaCl, обработанных электрическими импульсами амплитудой 100 мВ с частотой следования 400 и 440 Гц.

Однако существует ряд частот следования импульсов, при которых обработка электрическими импульсами приводит к неравномерному временному поведению I(t), т. е. эффект обработки аналогичен добавлению пиперина в жидкий образец. Были обнаружены следующие характерные выделенные частоты: 82,5, 174 и 417 Гц. Значения этих частот подчиняются примерному соотношению 1 : 2 : 5. Возможно, существуют еще какие-то особые частоты, просто мы их пока не нашли. Мы также не знаем физического механизма, стоящего за эффектами, связанными с этими частотами. Здесь и далее для определенности ограничимся случаем частоты повторения 417 Гц и изотонического раствора NaCl. На рис. 6 (а) и (б) (ср. графики на рис. 5 для частот 400 и 440 Гц) показаны зависимости в нескольких последовательных экспериментах, проведенных с интервалом в две недели в разных лабораториях; расстояние между этими лабораториями составляет примерно 20 км. Интервалы между началом измерений для каждого эксперимента обозначены буквой τ. Очевидно, что нет хорошей воспроизводимости от измерения к измерению, поэтому доверительные интервалы не показаны. Также приводятся результаты расчетов коэффициента ранговой корреляции Пирсона R между графиками.

Результаты спектрально-корреляционной обработки экспериментальных кривых, представленных на рис. 6, представлены на рис. 7 — 9. На рис. 7 представлены зависимости A(f), представляющие собой результат преобразования Фурье I(t), показанный на рис. 6 (б) для различных τ; эти зависимости получены с помощью вейвлет-преобразования Морле, см. [35].

В нашем конкретном случае вейвлет Морле задается формулой ψ (t) = exp (−t²/ 2) cos (5t) . Здесь A(f) — спектральная амплитуда на частоте f. Видно, что на всех кривых имеется спектральный максимум на частоте  ~ 4 x 10⁻⁴ Гц. Также видно, что на частоте f → 0 зависимость A(f) расходится, что связано со спецификой вейвлет-преобразований с использованием вейвлета Морле на сверхнизких частотах (см. [35]), т.е. функцией A(f) на низких частотах можно пренебречь.

При дальнейшем анализе из зависимостей A(f) был выделен участок A(f) с  изолированным спектральным максимумом, и для этого участка была найдена спектральная плотность A²(f), которая, в свою очередь, аппроксимировалась лоренцевой зависимостью

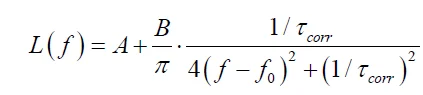
Здесь A и B — константы, f₀ — центральная (резонансная) частота, τcorr — время корреляции случайного процесса с лоренцевой спектральной линией; ширина лоренцевого контура ∆f ~ (τcorr)⁻¹, см. [36]. На рис. 8 представлена зависимость A² (f) для кривой A(f), показанной на рис. 7, для τ = 52,5 ч. На рис. 9 (а) и (б) представлены зависимости коэффициента ранговой корреляции Пирсона R от времени τ. Подробное описание методов расчета коэффициента ранговой корреляции Пирсона можно найти по гиперссылке [37]. В нашем случае коэффициент корреляции Пирсона применительно к выборке описывается формулой

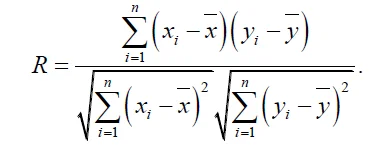
Здесь n — размер выборки, Xi и yi — отдельные точки выборки, индексированные с i,

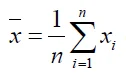
(среднее значение выборки; аналогично для y ). В формуле (5) набор значений xi соответствует первому измерению I(t) на рис. 6 (обозначен символом (1) на графиках), а набор значений yi соответствует измерению I(t) через время τ. Как следует из уравнения (5), R(τ = 0) = 1.

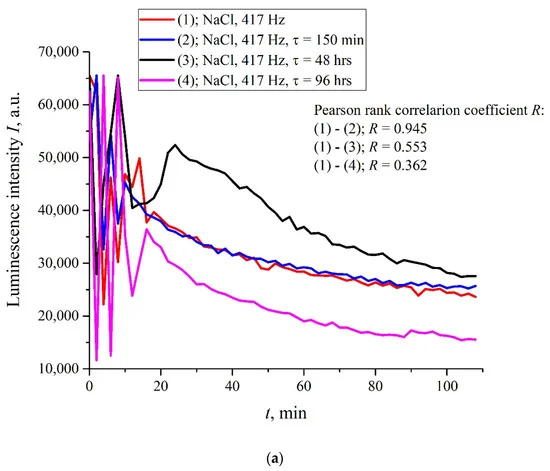
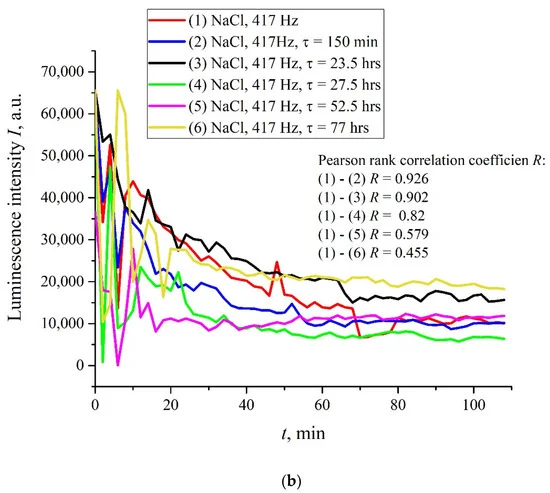
Рисунок 6. Интенсивность I(t) для изотонического раствора NaCl после обработки при частоте следования импульсов 417 Гц. Отличие графиков на панелях (а) и (б) состоит в том, что 363 измерения проводились в разных лабораториях; расстояние между лабораториями 20 км. Здесь τ – интервал времени между началом соответствующих измерений. Для всех значений τ рассчитывали коэффициент ранговой корреляции Пирсона.

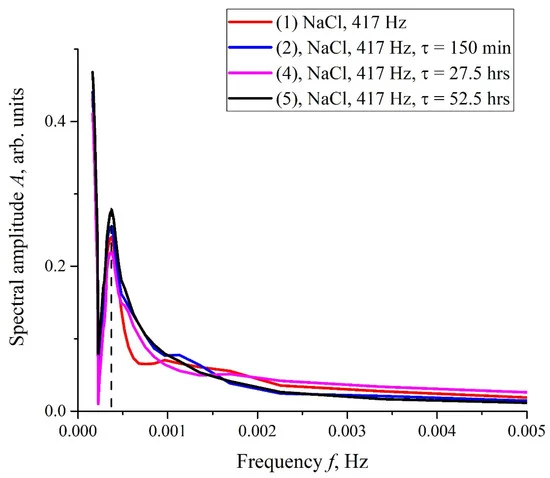
Рисунок 7. Результаты преобразования Фурье зависимостей I(t), представленных на рис. 6 (б). Частотные зависимости спектральной амплитуды A(f) были получены с помощью вейвлет-преобразования Морле. Пунктирной линией отмечена центральная частота спектрального максимума.

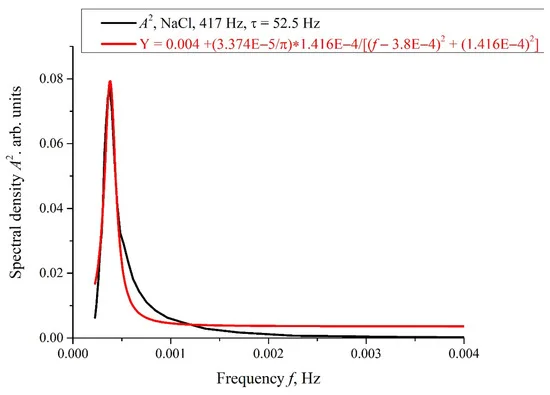
Рисунок 8. Спектральная плотность A²(f) для зависимости A(f) при τ = 52,5 ч на рис. 7. Эта зависимость аппроксимирована лоренцевской, см. уравнение (4).

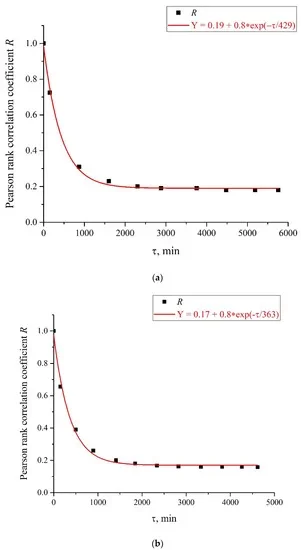
Рисунок 9. Коэффициент ранговой корреляции Пирсона R(τ) для кривых на рис. 6. Панель (а) относится к кривым на рис. 6 (а), а панель (б) – к кривым на рис. 6 (б).

Кроме того, в некоторых экспериментах колбу с жидким образцом оборачивали алюминиевой фольгой толщиной 10 мкм и обрабатывали образец электрическими импульсами с частотой следования 417 Гц. Результаты этого эксперимента представлены на рис. 10. Видно, что в данном случае стохастического поведения не наблюдалось, а интенсивность люминесценции I(t) с хорошей точностью совпадает с эталонной кривой. Это вполне ожидаемо: эффект обработки в этом случае отсутствует из-за экранирования жидкого образца.

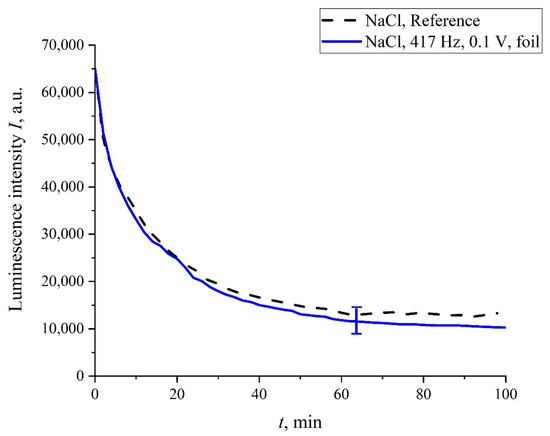
Рисунок 10. Зависимость I(t) после обработки при частоте следования импульсов 417 Гц для раствора NaCl; жидкий образец во время обработки был обернут алюминиевой фольгой толщиной 10 мкм.

Кроме того, в некоторых экспериментах мы покрывали фотолюминесцентную установку (см. рис. 2) алюминиевой фольгой толщиной 10 мкм; в этих же опытах изучали люминесценцию Нафиона, набухшего в изотоническом растворе NaCl при воздействии электрических импульсов частотой 417 Гц. На рис. 11 представлены два графика, полученные в ходе одного эксперимента: без экрана из фольги и с экраном. Видно, что при экранировании установки стохастическое поведение отсутствует, а интенсивность люминесценции I(t) близка к эталонной кривой. Однако при снятии экрана вновь появлялись стохастические скачки сигнала люминесценции. Такое поведение можно объяснить действием внешней случайной силы электромагнитной природы, проявляющейся в ходе эксперимента по люминесцентной спектроскопии.

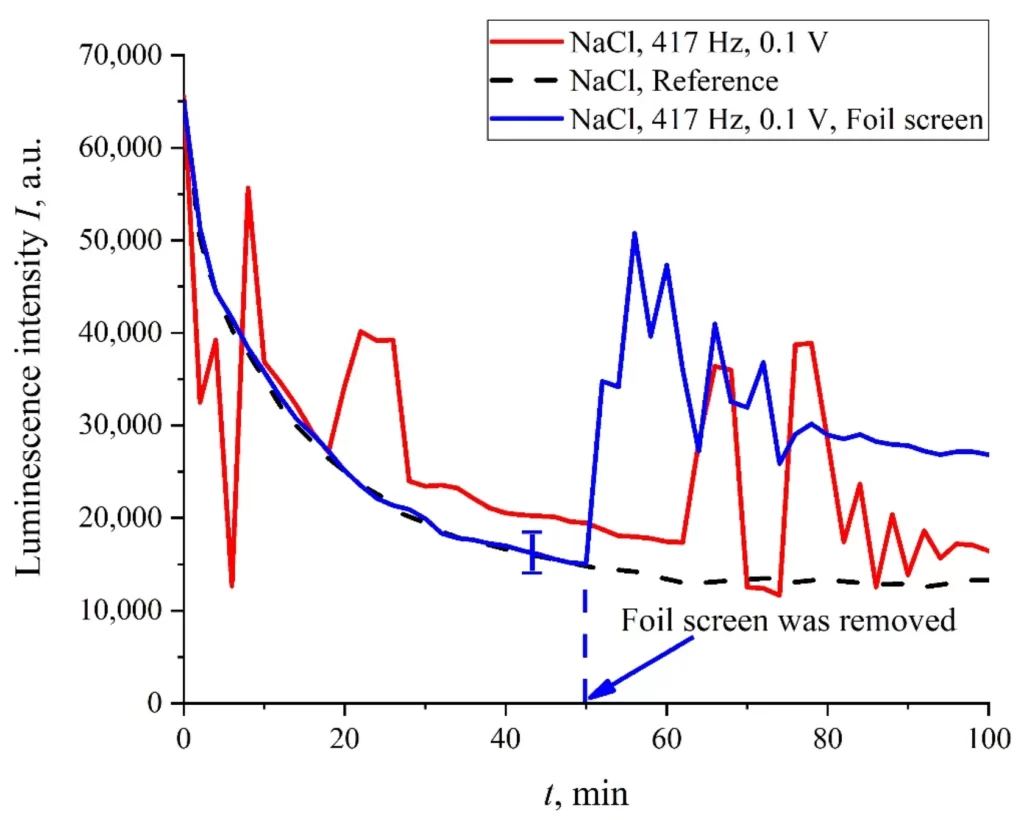
Рисунок 11. Зависимость I(t) после обработки при частоте следования импульсов 417 Гц для раствора NaCl; фотолюминесцентная установка закрывалась экраном из алюминиевой фольги толщиной 10 мкм (синяя кривая) или не закрывалась экраном (красная кривая). Стохастическое поведение восстанавливается сразу после удаления экрана.

Как было сказано во введении, в процессе набухания полимерные волокна эффективно раскручиваются в объеме жидкости, но не отрываются полностью от поверхности, т. е. образуется жесткая щеткообразная структура; длина площади, занятой размотанными волокнами, составляет сотни микрон.

Как показано в [16], эффект раскручивания зависит от содержания дейтерия в жидком образце. Фактически этот эффект отсутствует в так называемой воде, обедненной дейтерием (DDW, 413 содержание дейтерия ≤ 1 ч./млн). Таким образом, необходимо провести эксперимент по люминесценции с жидким образцом на основе DDW. На рис. 12 представлена интенсивность люминесценции I(t) в изотоническом растворе NaCl на основе DDW. Видно, что стохастических колебаний не наблюдается, т. е. интенсивность люминесценции I(t) с хорошей точностью совпадает с эталонной кривой.

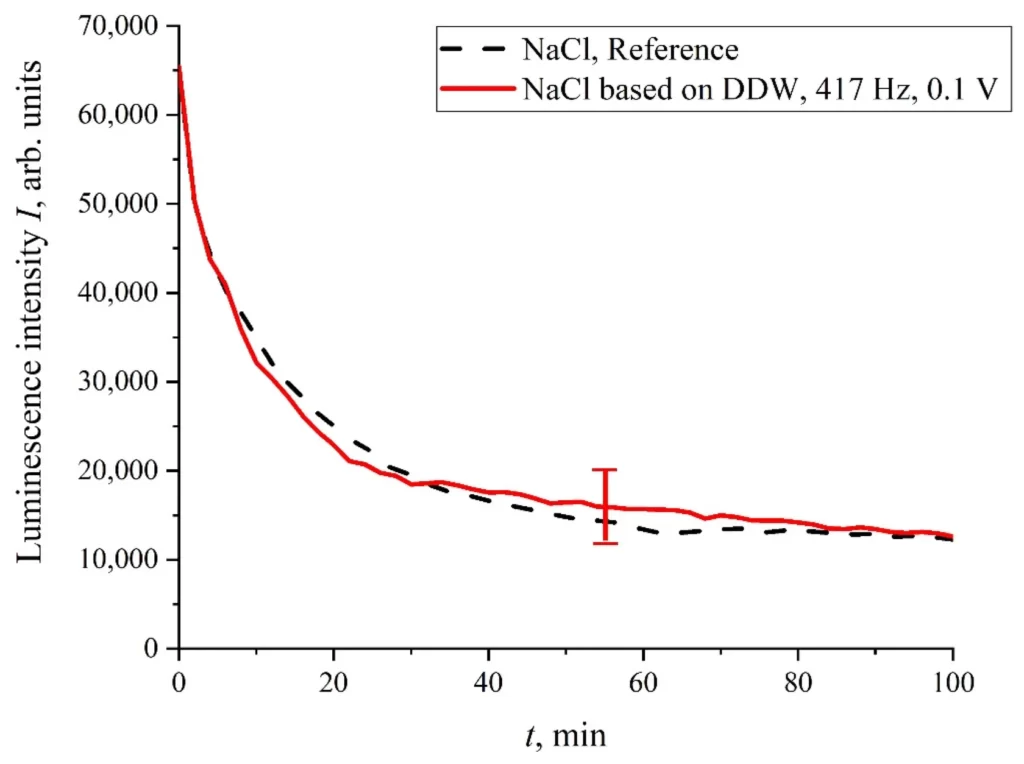
Рисунок 12. Зависимость I(t) в растворе NaCl на основе DDW, обработанном электрическими импульсами с частотой следования 417 Гц.

4. ОБСУЖДЕНИЕ

Стохастическое поведение интенсивности I(t), показанное на графиках рис. 6, можно объяснить эффектами, связанными с внешним низкочастотным электромагнитным полем. Это следует из того, что случайный характер I(t) исчезает при экранировании экспериментальной установки алюминиевой фольгой (см. рис. 11), но вновь появляется при снятии экрана. Как следует из графика на рис. 8, центр спектральной плотности этой электромагнитной волны приходится на частоту f₀ = 429 3,8 х 10⁻⁴ Гц, а ширина спектральной линии на полувысоте составляет ∆f = 1,416 х 10⁻⁴ Гц (см. вставку на рис. 8). Величина ∆f согласуется с зависимостями коэффициента корреляции R(τ), см. рис. 9 (а) и (б). Как видно на рис. 9 (а) и (б), экспериментальные точки хорошо ложатся на убывающую экспоненциальную функцию R(τ) ~ exp(-433 τ/τcorr), где τcorr – время затухания (время корреляции). Как следует из графиков на рис. 9, не имеет значения, с какого момента времени мы начали измерения I(t). Кроме того, полученные результаты не зависят от пространственного положения экспериментальной установки. Таким образом, мы, по-видимому, имеем дело со стационарной и пространственно-однородной внешней электромагнитной волной. Как следует из теоремы Винера-Хинчина [36], зависимость R(τ) ~ exp(-τ/τcorr) соответствует спектральной плотности случайного процесса, описываемого лоренцевым контуром ширины ∆f ~ (τcorr)⁻¹. Для диаграммы, представленной на рис. 9 (а), имеем τcorr = 25740 с, а ∆f ≈ ∆f ≈ 0,4 х 10⁻⁴ Гц. Для диаграммы на рис. 9 (б) имеем τcorr = 21780 с, а ∆f ≈ 0,5х10⁻⁴ Гц. Таким образом, значения ∆f, полученные на основании данных графиков рис. 8 и 9, одного порядка. Мы до сих пор не знаем, почему такое стохастическое поведение проявляется только при определенных частотах обработки жидких образцов.

На наш взгляд, внешний источник электромагнитного излучения, благодаря которому возникают описанные выше эффекты, может быть связан с пульсациями удаленных космических объектов. В этой связи необходимо упомянуть недавно опубликованную статью [38], посвященную открытию неизвестного явления, порождающего гигантский выброс энергии с регулярным временным интервалом 18,18 мин. Это космическое явление не похоже ни на что, с чем ученые сталкивались раньше. Исследователи считают, что загадочным источником вспышек является нейтронная звезда или белый карлик со сверхмощным магнитным полем. Этот объект, возможно, вращается, испуская луч излучения, который становится очень ярким радиоисточником в течение 30-60 секунд. Сам объект находится на расстоянии около четырех тысяч световых лет от Земли. Как показано в [37], этот объект может быть магнетаром с очень большим периодом и экстремально сильным магнитным полем. Этот объект, вероятно, эффективно преобразует магнитную энергию в радиоволны. Частоты радиоволн, излучаемых при вспышках минутной длительности, лежат в диапазоне 80—220 МГц, и это излучение линейно поляризовано.Напомним, что эти вспышки происходят с частотой 1/18,18 мин⁻¹ = 9 х 10⁻⁴ Hz ≈ 2f₀. Поэтому мы не можем утверждать, что источник радиоволн, приводящий к стохастическому поведению I(t), соответствует описанному в [38]. Для нас очень важно, что такие источники действительно существуют.

Поэтому без ограничения общности будем считать, что мы имеем дело с импульсами линейно поляризованной электромагнитной волны частотой 100 МГц; частота следования этих импульсов f₀ = 3,8 х 10⁻⁴ Гц.
Сначала покажем, что в воде отсутствует поглощение электромагнитной волны на частоте ω = 100 МГц. Как известно из [39], взаимодействие внешней электромагнитной волны со средой описывается комплексной диэлектрической проницаемостью ε = ε’ — iε», где действительная часть ε’ описывает «способность» среды поляризоваться внешнее поле, а мнимая часть ε» описывает потери энергии, связанные с поглощением и преобразованием в тепло. Для коэффициентов ε’ и ε» имеем

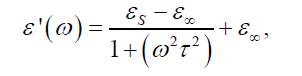
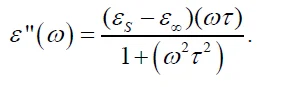
Здесь τ – время вращательной диффузии молекул воды,

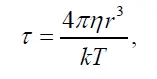
εs — статическая диэлектрическая проницаемость (для воды εs = 81), ε∞ — диэлектрическая проницаемость в оптическом диапазоне (для воды ε∞ = 1,77), r — молекулярный радиус (для воды r = 1,38 Å), η — динамическая вязкость (для воды η = 8,9 x 10⁻⁴ Па·с). После замен воды при нормальных условиях получаем τ ≈ 8,27 Па•с. Отсюда следует оценка ωτ ≈ 8,310⁻⁴, т. е. , ε» << ε’ ≈ εs, и поглощением на этой частоте можно пренебречь. 
Как следует из рис. 6 и 12, для возникновения стохастических колебаний необходимо, чтобы при набухании мембраны волокна полимера разматывались в объем жидкости. Напомним также, что эксперименты по фотолюминесцентной спектроскопии начинаются примерно через 20 минут после окончания обработки жидкости электрическими импульсами.

Ниже представлена качественная модель, описывающая возникновение стохастических колебаний с учетом эффектов длительной релаксации жидких образцов, а также с учетом разматывания полимерных волокон.Как показано в нашей недавней работе [40], если жидкость насыщена растворенным газом (например, атмосферным воздухом) и имеет ионную составляющую, то в ней спонтанно возникают газовые нанопузырьки.

Эти нанопузырьки стабилизируются за счет адсорбции аниона на внутренней (со стороны газовой фазы) поверхности нанопузырьков. Такие нанопузырьки были названы бабстонами (аббревиатура от «пузырек, стабилизированный ионами»). При рассмотрении стабилизации бабстонов за счет ионной адсорбции необходимо учитывать, что отрицательно заряженные (за счет адсорбции анионов) газовые ядра всегда окружены сферически-симметричным диффузионным облаком противоионов (дебаевское экранирование). При движении бабстонов в вязкой жидкости периферийные слои этого облака эффективно «размываются», а бабстоны заряжаются отрицательно. Действительно, при электрофорезе пузырьки движутся к аноду, см. [41 – 43]; о методах измерения электрофоретической подвижности частиц см. также [44 – 46]. Отметим, что в водных растворах солей с достаточно высокой концентрацией ионов отдельные бабстоны способны коагулировать друг с другом с образованием кластеров бабстонов микронного размера. Как показано в [47], бабстоны, двигаясь в вязких растворах электролитов, приобретают противоположные знаки, что приводит к их коагуляции за счет центрально-симметричной кулоновской силы притяжения.

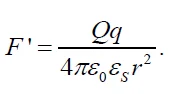
Здесь Q — заряд бабстона, который можно оценить на основании результатов экспериментов с динамическим светорассеянием и измерений ζ-потенциала, см. [40]. Получаем Q ~ 10⁻¹⁷ Кл, т.е. заряд бабстона составляет около сотни элементарных зарядов. Другие параметры в формуле (9) следующие: r — радиус бабстонного кластера (~ 1 мкм), q — эффективный заряд центра, притягивающий бабстон в процессе коагуляции. Таким образом, мы получаем формулу F’~10⁻¹⁴N. Здесь мы не знаем точного значения заряда q; в уравнении (9) предположим, что q ~ −Q. Однако, поскольку кластер представляет собой совокупность димеров, состоящих из частиц противоположного знака, заряд q следует рассчитывать как сумму членов чередующегося ряда. Таким образом, скорее всего, |q|<< |Q|, т. е. F’<< 10⁻¹⁴ Н.

Ясно, что за счет взаимодействия (9) должен образоваться сферически-симметричный бабстонный кластер. Экспериментальные исследования бабстонных кластеров в водных растворах NaCl представлены в [48]; оказалось, что кластерная фаза проявляется в опытах при концентрациях ионов > 0,1 М.

Очевидно, что этому условию удовлетворяют изотонические растворы NaCl и Рингера, в то время как в деионизированной воде концентрация ионов меньше, а кластерная фаза отсутствует. Действительно, по нашим измерениям, значение рН в деионизированной воде равно 5,7, т. е. содержание ионов равно 10⁻⁶ М, что недостаточно для коагуляции бабстонов, а кластеры не проявляются в опытах с динамическим рассеянием света в воде.Характерное время жизни бабстонов/кластеров бабстонов было измерено в [40].

В этом эксперименте измеряли распределение рассеивателей по размерам в 1 М в растворе NaCl, а затем жидкий образец отстаивали в течение 6 месяцев в стационарных условиях в герметично закрытой (без доступа атмосферного воздуха) кювете 2 см в высоту.

Оказалось, что микронные рассеиватели (бабстонные кластеры) после такого длительного отстаивания исчезают, а субмикронные рассеиватели (отдельные бабстоны) остаются в жидкости («выживают»). Исчезновение крупных рассеивателей, очевидно, связано с их всплытием и последующим разрушением на поверхности жидкости, тогда как отдельные бабстоны имеют нейтральную плавучесть, т. е. не всплывают. Таким образом, можно утверждать, что бабстоны являются равновесной фазой водного раствора электролита при нормальных условиях, а бабстонные кластеры — долгоживущей фазой.Предположим теперь, что однородное электрическое поле плоского конденсатора, используемого для обработки жидких образцов, имеет напряженность E ~ 1 544 В/м (напряжение составляло ~ 0,1 В).

Таким образом, в плоском конденсаторе возникает сила F = QE ~ 10⁻¹⁷ Н, которая накладывается на сферически-симметричную кулоновскую силу (9). Принимая F’ ~ 10⁻¹⁴ Н, мы имеем F/F’ ~ 10⁻³, но это значение, по-видимому, занижено, см. выше. Принимая F’ ≈ F, получаем, что сила F, возникающая внутри плоского конденсатора, может нарушать сферическую симметрию бабстонных кластеров, и кластер становится слегка анизотропным. Косвенно это подтвердилось в эксперименте с обработкой раствора NaCl частотой 417 Гц; при этом использовался один плоский конденсатор (см. рис. 13, а)) или два плоских конденсатора, установленных перпендикулярно друг другу (рис. 13, б).

Зависимость I(t) представлена на рис. 13 (в). Как следует из графиков рис. 13 (в), при использовании одного плоского конденсатора интенсивность люминесценции I(t) ведет себя стохастически (красная кривая), а при обработке двумя взаимно перпендикулярными конденсаторами (синяя кривая) I(t) близка к эталонной зависимости.

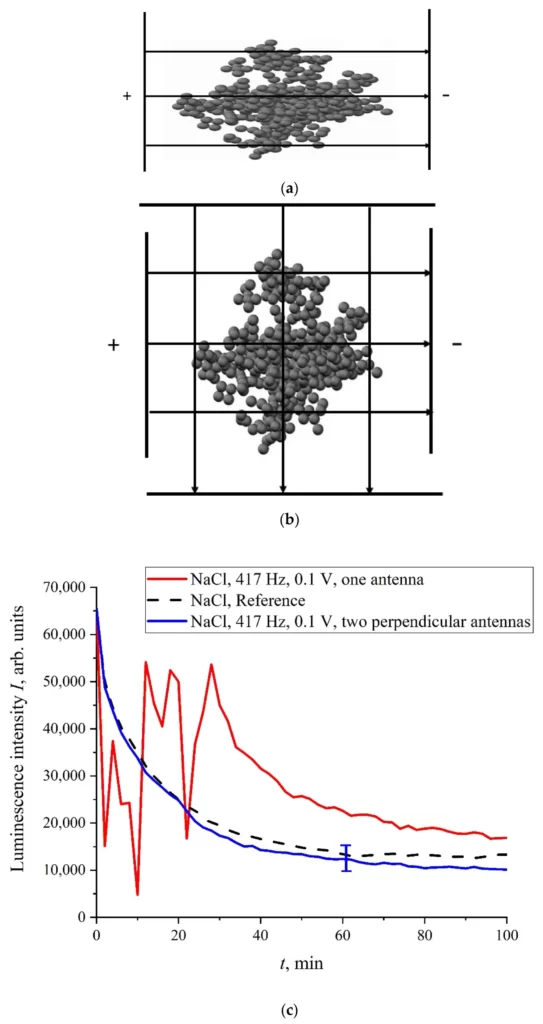
Рисунок 13. Панель (а) – схема обработки с одним конденсатором. Панель (б) – схема обработки с двумя конденсаторами. Панель (в) — зависимость I(t); раствор NaCl предварительно обрабатывали электрическими импульсами частотой 417 Гц с использованием одного/двух 566 взаимно перпендикулярных плоских конденсаторов. Красная кривая относится к одному конденсатору, а синяя кривая относится к двум конденсаторам.

Очевидно, что когда мы имеем дело с двумя перпендикулярными конденсаторами, внешнее электрическое поле не имеет фиксированной оси, т. е. это поле не изменяет сферичность бабстонного кластера. При этом интенсивность люминесценции близка к эталонной зависимости, которая достаточно хорошо воспроизводится. Если обработка происходит в поле одного плоского конденсатора, то поведение I(t) носит случайный характер. Таким образом, для эффекта памяти необходимо изменить геометрию кластера: кластер должен быть слегка анизотропным, и эти анизотропные свойства должны сохраняться достаточно длительное время.

Действительно, какие-либо физические механизмы релаксации анизотропного кластера к его сферической симметрии, по-видимому, отсутствуют.Представим себе, что внешнее линейно поляризованное излучение на частоте 100 МГц рассеивается бабстонными кластерами. Если кластеры сферически симметричны, то рассеянное излучение останется линейно поляризованным. Однако если кластеры анизотропны, рассеянное излучение будет деполяризованным, см., например, [49]. Конечно, следует иметь в виду, что сечение рассеяния σsca в этом случае будет очень мало, так как σsca ~ 1/λ⁴ [39], а λ ~ 1 м. Рассеянное излучение будет взаимодействовать с размотанными в объеме жидкости заряженными полимерными волокнами. Нам не известны масса и заряд этих волокон, поэтому мы не приводим формул, описывающих динамику этих волокон в поле падающей волны.

Однако, согласно литературным данным, излучение на частотах этого диапазона используется в медицинской практике (в частности, для лечения онкологических заболеваний), причем это излучение относится не только к электромагнитным волнам, но и к акустическим волнам, см. [50, 51]. На основании этих косвенных данных можно утверждать, что размотанные в объем жидкости полимерные волокна будут колебаться с частотой 100 МГц. В случае линейно поляризованного излучения эти колебания будут происходить в одной плоскости, а в случае деполяризованного излучения колебания будут происходить в разных плоскостях.Как следует из уравнения (1), если сечение люминесценции σlum не меняется при набухании, то интенсивность люминесценции I(t) падает экспоненциально.

Таким образом, стохастическое поведение можно объяснить случайными колебаниями σlum. Для объяснения этого эффекта на качественном уровне необходимо использовать модель безызлучательного переноса энергии от донора люминесценции к акцептору люминесценции, см. монографию [52]. Представим себе, что на поверхности мембраны существует центр люминесценции, который мы назовем донором люминесценции.

Представим далее, что на некотором расстоянии R от донора существует другая частица (акцептор люминесценции), спектр поглощения которой совпадает со спектром поглощения донора. Тогда при определенном R возможен процесс резонансной передачи энергии с донорного люминесцентного уровня на акцепторный. Электрон с акцепторного уровня переходит в основное состояние акцептора, что может сопровождаться испусканием фотона (люминесценцией), но возможен и безызлучательный переход. В этом случае люминесценция от донора гасится. Если рассматривать белковые мембраны, то донорами и акцепторами, как правило, являются одни и те же группы белков, но в случае акцепторов эти группы несколько изменены, см. [52]. Поскольку в нашем случае центрами люминесценции являются сульфогруппы, можно предположить, что акцептором является слабомодифицированная сульфогруппа, не активная в отношении люминесценции. Эффективность S передачи энергии от донора к акцептору определяется как

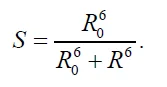
Здесь R₀ = 30 — 60 Å — так называемый параметр Форстера, см. [52]. Таким образом, значение S изменяется как R⁻⁶, т.е. это очень крутая функция. Отметим, что если донор и акцептор жестко закреплены на поверхности мембраны, то расстояние R между ними всегда фиксировано, т. е. сечение люминесценции σlum не изменяется при набухании. Однако в нашем случае донор и акцептор находятся на размотанных в объеме жидкости полимерных волокнах, т.е. их пространственное положение может изменяться за счет каких-то внешних электромагнитных сил (напомним, что сульфогруппы заряжены).

Если эти силы изменяют расстояние R, то согласно уравнению (10) значение S может быть либо ~ 1, и люминесценция прекращается (эффект тушения), либо S << 1, и в этом случае передачи энергии нет, а люминесценция достаточно интенсивна. Таким образом, в наших экспериментах единственным механизмом, благодаря которому люминесценция может исчезнуть/появиться вновь в растворах NaCl на основе природной воды, является изменение расстояния R, что приводит к колебаниям σlum. Представляется очевидным, что когда полимерные волокна, намотанные в объем жидкости, возбуждаются линейно поляризованным излучением, эти волокна будут колебаться в одной плоскости. При этом расстояние R между донором и акцептором не меняется, т. е. значение σlum остается постоянным.

В то же время, если эти волокна приводятся в колебание деполяризованным излучением, то есть существуют поляризации в разных плоскостях, то расстояние R будет изменяться хаотично, и возможно стохастическое переключение режимов тушения/возбуждения люминесценции. В рамках этой модели качественно объясняется появление стохастических явлений в наших экспериментах. Остается неясным вопрос, почему добавление пиперина также приводит к стохастизации поведения I(t).Можно предположить, что случайные колебания I(t) могут возникать и при механических возмущениях разматываемых полимерных волокон.

Чтобы проверить это, был проведен следующий эксперимент. Мы исследовали бидистиллированную воду, в которой содержание бабстонов очень мало, а кластерная фаза практически отсутствует; жидкие образцы не обрабатывались электрическими импульсами. В кювету (не показана на рис. 2), в которой пропитывалась мембрана Нафион, вводили капилляр толщиной 0,5 мм. Через 40 мин выдержки через этот капилляр в кювету нагнетали атмосферный воздух. Это сопровождалось образованием пузырьков, которые всплывали на поверхность воды и генерировали на поверхности поперечную капиллярную волну. На рис. 14 показана зависимость I(t). Видно, что до нагнетания пузырьков кривая I(t) с хорошей точностью совпадает с эталонной зависимостью. Как только возбуждалась поперечная капиллярная волна, начинались осцилляции I(t); в определенный момент времени сигнал люминесценции падал до нуля. Очень важно, что в этом опыте мембрана Нафиона была полностью погружена в объем воды.

Как известно, поперечные звуковые волны очень сильно затухают в объеме жидкости, см. [53]. Тем не менее генерация поперечной волны на поверхности сопровождалась колебаниями I(t) в объеме жидкости. Эта волна должна быть очень слабой в объеме, но тем не менее она может изменить расстояние R между донором и акцептором на размотанных полимерных волокнах.

Можно утверждать, что Нафион является высокочувствительной полимерной матрицей: очень слабая внешняя сила, которая может изменить расстояние R, приводит к заметному изменению поведения I(t). Поэтому деполяризованное рассеянное излучение приводит к эффектам стохастизации, несмотря на очень малое сечение рассеяния σsca.

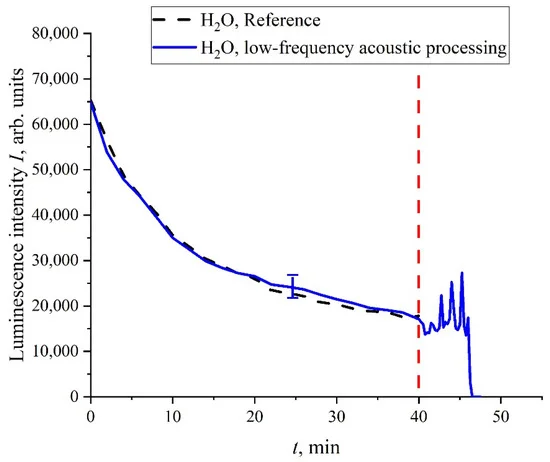
Рисунок 14. Зависимость I(t) в воде; атмосферный воздух откачивали через 40 минут выдержки.

5. ВЫВОДЫ

Наиболее интересным результатом работы является наблюдение стохастических режимов интенсивности люминесценции I(t) при набухании полимерной мембраны в водно-солевых растворах, подвергнутых воздействию электрических импульсов с определенной частотой следования.

Для возникновения стохастических режимов необходимо воздействие внешней случайной силы. Было показано, что эта сила имеет электромагнитную природу. По нашей гипотезе источником этой силы могут быть регулярные вспышки далеких космических объектов. Спектральная и корреляционная обработка временных зависимостей I(t) показывает, что источником внешней электромагнитной волны могут быть пульсации магнетаров или белых карликов, описанные в недавней работе [38].

Эффекты стохастизации наблюдаются только в том случае, если полимерные волокна в процессе набухания полимера разматываются в объеме жидкости. Создана качественная теоретическая модель, согласно которой стохастическое поведение I(t) возникает из-за случайных изменений сечения люминесценции σlum. Эти изменения происходят из-за того, что жидкие образцы содержат бабстонные кластеры, которые в результате обработки электрическими импульсами приобретают анизотропные свойства.

Падающее линейно поляризованное низкочастотное излучение, рассеиваясь в жидких образцах, становится деполяризованным. При этом полимерные волокна, размотанные в объем жидкости, испытывают колебания в поле внешней волны в разных плоскостях, что приводит к изменению среднего расстояния между этими волокнами. Предполагается, что в нашем случае возможны эффекты резонансного переноса энергии люминесценции между донором и акцептором, а расстояние R между донором и акцептором, локализованными на размотанных волокнах, изменяется случайным образом. В рамках этой качественной модели можно объяснить эффекты стохастизации, возникающие в наших экспериментах.

ЛИТЕРАТУРА

1. Mauritz, K.A.; Moore, R.B. State of understanding of Nafion. Chem. Rev. 2004, 104, 4535–4585.
2. Choi, J.S.; Tsui, J.H.; Xu, F.; Lee, S.H.; Sung, S.K.; Lee, H.J.; Wang, C.; Kim, H.J.; Kim, D.H. Fabrication of Micro- and Nanopatterned Nafion Thin Films with Tunable Mechanical and Electrical Properties Using Thermal Evaporation-Induced Capillary 708 Force Lithography, Adv. Mat. Int., 2021, 8, 2002005.
3. Ye, J.Y.; Yuan, D.; Ding, M.; Long, Y.; Long, T.; Sun, L.D.; Jia, C.K. A cost-effective nafion/lignin composite membrane with low vanadium ion permeation for high performance vanadium redox flow battery, J. Power Sources, 2021, 482, 229023.
4. Castelino, P.; Jayarama, A.; Bhat, S.; Satyanarayan; Fernandes, P.; Prabhu, S.; Duttagupta, S.; Pinto, R. Role of UV irradiated Nafion in power enhancement of hydrogen fuel cells, Int. J. Hydrogen Energy, 2021, 46, 25596-25607.
5. Shinkawa, M.; Motai, K.; Eguchi, K.; Takarada, W.; Ashizawa, M.; Masunaga, H.; Ohta, N.; Hayamizu, Y.; Matsumoto, H. Preparation of Perfluorosulfonated Ionomer Nanofibers by Solution Blow Spinning, Membranes, 2021, 11, 389.
6. Lufrano, E.; Simari, C.; Di Vona, M.L.; Nicotera, I.; Narducci, R. How the Morphology of Nafion-Based Membranes Affects Proton Transport, Polymers, 2021, 13, 359.
7. Chen, C.S.; Chung,W.J.; Hsu, I.C.; Wu, C.M.; Chin,W.C. Force field measurements within the exclusion zone of water. J. Biol. Phys. 2011, 38, 113–120.
8. Huszár, I.; Mártonfalvi, Z.; Laki, A.; Iván, K.; Kellermayer, M. Exclusion-Zone Dynamics Explored with Microfluidics and Optical Tweezers. Entropy, 2014, 16, 4322–4337.
9. Spencer, P.D.; Riches, J.D.; Williams, E.D. Exclusion zone water is associated with material that exhibits proton diffusion, but not birefringent properties. Fluid Phase Equilibria 2018, 466, 103–109.
10. Figueroa, X.A.; Pollack, G.H. Exclusion-zone formation from discontinuous nafion surfaces. Int. J. Des. Nat. Ecodyn. 2011, 6, 286–296.
11. Pollack, G.H. The Fourth Phase of Water; Ebner and Sons Publishers: Seattle, WA, USA, 2013.
12. Pedregal-Cortés, R.; Toriz, G.; Delgado, E.; Pollack, G.H. Interfacial water and its potential role in the function of sericin against biofouling. Biofouling 2019, 35, 732–741.
13. Florea, D.; Musa, S.; Huyghe, J.M.R.; Wyss, H.M. Long-range repulsion of colloids driven by ion exchange and diffusiophoresis. Proc. Natl. Acad. Sci. USA 2014, 111, 6554–6559.
14. Ball, P. Water as an Active Constituent in Cell Biology. Chem. Rev. 2008, 108, 74–108.
15. Elton, D.C.; Spencer, P.D.; Riches, J.D.; Williams, E.D. Exclusion zone phenomena in water — A critical review of experimental findings and theories. Int. J. Mol. Sci. 2020, 21, 5041.
16. Bunkin, N.F.; Shkirin, A.V.; Kozlov, V.A.; Ninham, B.W.; Uspenskaya, E.V.; Gudkov, S.V. Near-surface structure of Nafion in deuterated water. J. Chem. Phys. 2018, 149, 164901.
17. Craig, H. Standard reporting concentrations of deuteriumand oxygen-18 in natural water. Science 1961, 133, 1833–1834.
18. Goodsell, D.S. The Machinery of Life; Springer Science + Business Media: Berlin/Heidelberg, Germany, 2009.
19. Reines, B.P.; Ninham, B.W. Structure and function of the endothelial surface layer: unraveling the nanoarchitecture of biological surfaces. Quarterly Reviews of Biophysics 2019, 52, e13, 1-11.
20. Jurak, M.; Wiącek, A.E.; Ładniak, A.; Przykaza, K.; Szafran, K. What affects the biocompatibility of polymers? Adv. Coll. Int. Sci. 2021, 294, 102451.
21. Panthong, S.; Imai, Y.; Matsuoka, T.; Suzuki, W.; Watanabe, T.; Terada, Y.; Kurohane, K.; Sekiguchi, K.; Ogawa, E.; Endo, Y.; Itharat. A. The role of Piper chaba Hunt. and its pure compound, piperine, on TRPV1 activation and adjuvant effect, BMC Complementary Medicine and Therapies 2020, 20, 134-144.
22. Beltrán, L.R.; Dawid, C.; Beltrán, M., Gisselmann, G.; Degenhardt, K.; Mathie, K.; Hofmann, T.; Hat, H. The pungent substances piperine, capsaicin, 6-gingerol and polygodial inhibit the human two-pore domain potassium channels TASK-1, TASK-3 and TRESK, Frontiers in Pharmacology 2013, 4, 141-152.
23. Adey, W.R. Tissue interactions with nonionizing electromagnetic fields. Physiol. Rev. 1981, 61, 435-514
24. Adey, W.R.; Lawrence, A.F. (eds.): Nonlinear Electrodynamics in Biological Systems. Plenum, New York 1984.
25. Chiabrera, A.; Nicolini, C.; Schwan, H.P. (eds.): Interactions Between Electromagnetic Fields and Cells. Plenum, NewYork 1985.
26. Polk, C.; Postow, E.(eds.): CRC Handbook of Biological Effects of Electromagnetic Fields. CRC, Boca Raton 1986. 
27. Blank, M.; Findl, E.(eds.): Mechanistic Approaches to Interactions of Electromagnetic Fields with Living Systems. Plenum, New York 752 1987.
28. Fröhlich, H. (ed.): Biological Coherence and Response to External Stimuli. Springer, Heidelberg 1988.
29. Wilson, B.W.; Stevens, R.G.; Anderson, L.E. (eds.): Extremely Low Frequency Electromagnetic Fields: The Question of Cancer. Batelle, Columbus 1991.
30. Saliev, T.; Begimbetova, D.; Masoud, A.R.; Matkarimov, B. Biological effects of non-ionizing electromagnetic fields: Two sides of a coin. Progress in Biophysics and Molecular Biology 2019, 141, 25-36.
31. Bunkin, N.F.; Bolotskova, P.N.; Bondarchuk, E.V.; Gryaznov, V.G.; Kozlov, V.A.; Okuneva, M.A.; Ovchinnikov, O.V.; Smoliy, O.P.; Turkanov, I.F. Long-Term Effect of Low-Frequency Electromagnetic Irradiation in Water and Isotonic Aqueous Solutions as Studied by Photoluminescence from Polymer Membrane, Polymers 2021, 13, 1443.
32. Eisenberg, D.; Kauzmann, W. The structure and properties of water, Oxford University Press 1969.
33. De Almeida, S.H.; Kawano, Y. Ultraviolet-visible spectra of Nafion membrane. Eur. Polym. J. 1997, 33, 1307–1311.
34. Quickenden, T.I.; Irvin, J.A. The ultraviolet absorption spectrum of liquid water. J. Chem. Phys. 1980, 72, 4416–4428.
35. Ashmead, J. Morlet Wavelets in Quantum Mechanics. Quanta 2012, 1, 58-70.
36. Vanmarcke, E. Random Fields, World Scientific, 2010.
37. https://mathworld.wolfram.com/CorrelationCoefficient.html (accessed on 2 February 2022).
38. Hurley-Walker, N.; Zhang; X.; Bahramian, A.; McSweeney, S.J.; O’Doherty, T.N.; Hancock, P. J.; Morgan, J.S.; Anderson, G.E.; Heald, G.H.; Galvin, T.J. A radio transient with unusually slow periodic emission. Nature 2022, 601, 526 – 530.
39. Landau. L.D.; Lifshitz, E.M. Course of Theoretical Physics, Vol. 8: Electrodynamics of Continuous Media, Pergamon Press 1960.
40. Bunkin, N.F.; Shkirin, A.V.; Suyazov, N.V.; Babenko, V.A.; Penkov, N.V.; Belosludtsev, K.N.; Gudkov, S.V. Formation and Dynamics of Ion-Stabilized Gas Nanobubble Phase in the Bulk of Aqueous NaCl Solutions. J. Phys. Chem. B 2016, 120, 1291–1303.
41. Kelsall, G.H.; Tang, S.Y.; Yurdakul, S.; Smith, A.L. Electrophoretic behaviour of bubbles in aqueous electrolytes. J. Chem. Soc. Faraday Trans. 1996, 92, 3887–3893.
42. Takahashi, M. Zeta-potential of microbubbles in aqueous solutions: Electrical properties of the gas-water interface. J. Phys. Chem. B 2005, 109, 21858–21864.
43. Ushikubo, F.Y.; Enari, M.; Furukawa, T.; Nakagawa, R.; Makino, Y.; Kawagoe, Y.; Oshita, S. Zeta-potential of Micro- and/or Nano-bubbles in Water Produced by Some Kinds of Gases. IFAC Proc. Vol. 2010, 43, 283–288
44. Dustan, D.E. The Electroforetic Mobility of Hydrocarbon Particles in KCl Solutions, Langmuir 2005, 21, 4347-4355.
45. Delgado A.V. Interfacial electrokinetics and electrophoresis; Ch. 32; Marcel Dekker, New York 2002.
46. Wiącek, A.E.; Anitowska, E.; Delgado, A.V.; Hołysz, L.; Chibowski, E. The electrokinetic and rheological behavior of phosphatidylcholine-treated TiO2 suspensions, Colloids Surfaces A 2014, 440, 110-115.
47. Bunkin, N.F.; Shkirin, A.V. Nanobubble clusters of dissolved gas in aqueous solutions of electrolyte. II. Theoretical interpretation. J. Chem. Phys. 2012, 137, 054707.
48. Bunkin, N.F.; Shkirin, A.V.; Ignatiev, P.S.; Chaikov, L.L.; Burkhanov, I.S.; Starosvetskiy, A.V. Nanobubble clusters of dissolved gas in aqueous solutions of electrolyte. I. Experimental proof. J. Chem. Phys. 2012, 137, 054706.
49. Van de Hulst, H.C. Light scattering by small particles. John Wiley and Sons, New York 1957. Choi, H.; Choe, S. Acoustic Stimulation by Shunt-Diode Pre-Linearizer Using Very High Frequency Piezoelectric Transducer for Cancer Therapeutics, Sensors 2019, 19, 357.
50. Brugger, M.S.; Baumgartner, K.; Mauritz, S.C.F.; Gerlach, S.C.; Röder, F.; Schlosser, C.; Fluhrer, R.; Wixforth, A.; Westerhausen, C. Vibration enhanced cell growth induced by surface acoustic waves as in vitro wound-healing model. PNAS 2020, 117, 31603–31613
51. Lakowicz, J.R. Principles of Fluorescence Spectroscopy; Ch. 13, Energy Transfer; Springer: Boston, MA, USA, 2006.
52. Landau, L. D.; Lifshitz, E. M. Course of Theoretical Physics, Vol. 6: Hydrodynamics; England Pergamon Press: Oxford, U.K., 1980.